キルヒホッフの法則 / Kirchoff's Laws

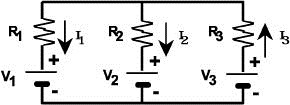
The diagram below shows a circuit where; R₁=6.00 Ω, R₂=2.00 Ω, R₃=3.00 Ω, V₁=2.00 V, V₂=9.00 V, and V₃=15.0 V. Find I₁, I₂, and I₃.

Problems like these aren't really hard, you just have to do the math correctly (Which I tend to mess up on).

Start with the Junction Rule, and pick a junction to define your current equation. Here we pick the top junction.

The Junction Rule states that all current entering a junction must equal all current exiting the junction. In order words:


I₁ + I₂ + I₃ = 0 (Equation 1)

It doesn't really make sense that all 3 currents go in the same direction, but the Junction Rule works regardless. Since they give you directions in the problem, we have to work with them, even if they seem counter-intuitive.

Now we use the Loop Rule (The sum of all potential changes is zero) to derive two more equations.

We start at the red dot and move counterclockwise, taking note of all potential changes. From the red dot to the orange dot, there is a potential increase, since we are moving through a resistor and we are opposing the current I_1.  From the orange dot to the yellow dot, there is a potential drop, since we are moving from the positive terminal of a battery to the negative terminal. From the yellow dot to the green dot, there is a potential increase, since we are moving from a negative terminal of a battery to the positive terminal. Finally, from the green dot to the blue dot, there is a potential drop, since we are moving through a resistor and we are moving with the current I_2.

In equation form then:

I₁R₁ – V₁ + V₂ – I₂R₂ = 0 (Equation 2)

Similarly, we do the same procedure again, with the other half of the circuit:

Using the same logic as before, we derive the equation:

I₂R₂ – V₂ + V₃ – I₃R₃ = 0 (Equation 3)

Notice that all 3 equations equal 0. This means we can equate them and solve for a particular variable, then use that variable to solve the rest.

Also notice that the variable I₂ is in each equation. Let us rearrange our equations so that they each have I₂ on one side:

I₁ + I₂ + I₃ = 0 (Equation 1)

-I₂ = I₁ + I₃

I₁R₁ – V₁ + V₂ – I₂R₂ = 0 (Equation 2)

I₁ = (V₁ – V₂ + I₂R₂) / R₁

I₂R₂ – V₂ + V₃ – I₃R₃ = 0 (Equation 3)

I₃ = (I₂R₂ – V₂ + V₃) / R₃

Finally, plug equation 2 and 3 into equation 1 and solve for I₂:

-I₂ = (V₁ – V₂ + I₂R₂) / R₁ + (I₂R₂ – V₂ + V₃) / R₁
-I₂ = 2/6 - 9/6 + (2/6)I₂ + (2/3)I₂ - 9/3 + 15/3
I₂ = -5/12 A (-0.417 A) 

We are almost done the problem. With I₂, we can find I₁ or I_3. Let's find I₃ first:

 I₃ = (I₂R₂ – V₂ + V₃) / R₁
 I₃ = [(-5/12)(2)]/6 - 9/6 + 15/6
 I₃ = 31/18 A (1.72 A)


All that's left is to find . We can do the same procedure as above, or we can use equation 1 and solve for the remaining variable. We will do the latter:


I₁ + I₂ + I₃ = 0
I₁ = I₂ - I₃ = 0
I₁ = -(-0.417) - 1.72
I₁ = -1.303 A


One final thing to note is that there is no such thing as a negative current; the negative signs merely denote that our initial guess in direction was incorrect. So a properly drawn diagram would therefore be: